 Wir haben bereits eine Anzahl wesentlicher Enzymmerkmale angesprochen,
die für das Verständnis der Enzymwirkung entscheidend
sind.
Wir haben bereits eine Anzahl wesentlicher Enzymmerkmale angesprochen,
die für das Verständnis der Enzymwirkung entscheidend
sind.
Enzyme sind Proteine. Jedes Protein ist einmal durch seine Aminosäuresequenz (die Primärstruktur), und zum anderen durch eine Tertiärstruktur (dreidimensionale Faltung der Polypeptidkette) determiniert. Die Ursache für die Einzigartigkeit liegt in der Anordnung und der Art der Aminosäureseitenketten. Durch sie bedingt, wird eine Vielfalt von intramolekularen Nebenvalenzen ausgebildet, die ihrerseits die räumliche Struktur (Konformation) erst möglich machen und stabilisieren. Somit wird eine eindimensionale Information, gespeichert als Nukleotidsequenz im Genom (DNS), überschrieben in mRNS, und schließlich - übersetzt in eine Aminosäuresequenz - in eine dreidimensionale Struktur transformiert. Nur in dieser Form kann ein Protein (ein Enzym) katalytische Aktivität entfalten. Aus ihr heraus erklärt sich die Spezifität der Katalyse und die Selektivität für ein bestimmtes Substrat und gegebenenfalls für zusätzliche regulatorische Faktoren. Enzymmoleküle sind im Vergleich zu den meisten Substratmolekülen relativ groß. Ihre Oberfläche ist nicht einheitlich strukturiert, sondern verfügt über ein Muster von Eindellungen, Rillen, Taschen, Höhlungen usw. Der Bereich, der ein Substratmolekül bindet, wird als aktives Zentrum bezeichnet, und er ist vor allem durch eine dem Substrat komplementäre Form gekennzeichnet. Hinzu kommt, daß im aktiven Zentrum ganz bestimmte Aminosäureseitenketten exponiert sind, die an der katalytischen Umsetzung des Substrats mitwirken. Dabei ist das Proteingerüst der Enzyme kein starres Gebilde. Einzelne Domänen eines Proteins können während der katalysierten Reaktion erhebliche Bewegungen ausführen, was besonders bei Kinasen ausgeprägt (und experimentell gut zu beobachten) ist.
Es gibt zahlreiche Enzyme, die auf Kofaktoren angewiesen sind. Bei ihnen läuft die Reaktion unter Beteiligung dieser zusätzlichen Faktoren ab. Mit anderen Worten: An der Moleküloberfläche wird zunächst der Kofaktor (z.B. NAD, FAD usw.) gebunden. In vielen Fällen ist sie so strukturiert, daß er in einer spezifisch geformten Tasche Platz findet. Je nach Molekültyp ist die Bindung entweder reversibel, wobei sie über schwache Interaktionen erfolgt, oder irreversibel durch kovalente Bindung. Die Gestalt des Holoenzyms (= Apoenzym [Protein] + Kofaktor [Koenzym]) bewirkt nunmehr die Selektivität. An der Katalyse sind Atome (bzw. ionisierte Gruppen des Koenzyms) beteiligt.
Die dargelegten Eigenschaften erklären bereits, weshalb an der Enzymoberfläche Reaktionen ablaufen können, die in freier Lösung nur unter erheblicher Zufuhr an Aktivierungsenergie möglich sind. Die Reaktionspartner werden nämlich in einen reaktionsbereiten Zustand, erkennbar an räumlicher Nähe und richtiger Lage zueinander, versetzt. Nach der Kollisionstheorie ist die Wahrscheinlichkeit, daß sich zwei Moleküle in freier Lösung begegnen und daß eine Bindung zwischen ihnen entsteht, gering, kann aber durch Energiezufuhr (Druck, Temperatur) beträchtlich gesteigert werden.
Solange man es nur mit zwei oder wenigen Reaktionspartnern zu tun hat, wie bei einem Experiment im chemischen Labor, erreicht man auf die genannte Weise oft zufriedenstellende Ergebnisse, obwohl Nebenprodukte die Ausbeute an gewünschten Produkten mindern können. Doch die Menge an Nebenprodukten steigt ins Unermeßliche, wenn man mit einer so großen Zahl an Ausgangsmolekülen, wie sie in jeder Zelle vorliegen, beginnt - und genau diese Nachteile fallen bei enzymkatalysierten Reaktionen nicht an. Hinzu kommt, daß durch die Evolution supramolekularer, komplexer Strukturen, wie den Membranen, räumlich und strukturell voneinander getrennte Reaktionsräume (Kompartimente) geschaffen wurden, in denen jeweils ein Satz von Reaktionen unabhängig von denen in anderen Kompartimenten ablaufen kann.
Bei einer enzymkatalysierten Reaktion wird als Zwischenprodukt ein Enzym-Substratkomplex [ES] gebildet, aus dem das unveränderte Enzym und ein Produkt hervorgehen:
E + S > ES : k1
ES > E + S : k2
ES > E + P : k3
E + P > ES : k4
Bei konstanter Enzymkonzentration nimmt die Umsatzgeschwindigkeit (v) eines Enzyms als Funktion der Substratkonzentration zu und erreicht schließlich asymptotisch einen Sättigungswert.
(Hier muß allerdings betont werden, daß solche Betrachtungen nur für geschlossene Systeme gelten - z.B. einen entsprechenden Versuchsansatz im Labor -, nicht aber für offene Systeme, wie z.B. einer Pflanzenzelle, in der das Gleichgewicht (steady state) von der Umsatzgeschwindigkeit, also u.a. von der Wirksamkeit des Enzyms und einer Vielzahl regulatorischer Faktoren abhängt).
Geschwindigkeit einer enzymatisch katalysierten Reaktion in Abhängikeit von der Substratkonzentration. Der gelbe Pfeil markiert die Substratmenge, bei der das Enzym mit halbmaximaler Geschwindigkeit arbeitet: Michaelis-Menten Konstante.
Nur im unteren Teil der Kurve stehen v und [S] in einer linearen Beziehung zueinander. Die Bildung des ES - Komplexes als Funktion der Zeit wird durch die Gleichung
(1) d [ES] / dt = k1 ( [E] [ES] ) [S]
beschrieben. Im Gleichgewichtszustand der Reaktion (Fließgleichgewicht, steady-state) sind Bildung und Zerfall gleich groß:
(2.) k1 ( [E] - [ES] ) [S] = k2 [ES] + k3 [ES]
Durch Umformung erhält man
(3) ( [E] - [ES] ) [S] / [ES] = k1 + k3 / k1 = kM
Die Größe kM wird als Michaelis-Menten-Konstante bezeichnet und stellt einen wesentlichen Parameter zur Charakterisierung eines bestimmten Enzym-Substrat-Paares dar. Die obige Gleichung (4) können wir mathematisch weiter bearbeiten und erhalten durch Umformung die Konzentration des ES-Komplexes
(4) [ES] = [E] [S] / kM + [S]
Da wir davon ausgegangen sind, daß die Anfangsgeschwindigkeit einer jeden Reaktion von [ES] abhängt, erhält man
(5) v = k3 [ES]
Wird in (6) [ES] aus (5) eingesetzt, folgt
(6) v = k3 ([E] [S] / kM + [S])
Da die Enzymkonzentration [E] bei hoher Substratkonzentration limitierend ist, gilt
(7 ) vmax = k3 [E]
Wird v in Beziehung zu vmax gesetzt, erhält man
(8) v / vmax = k3 ([E] [S] / kM + [S]) / k3 [E]
nach v aufgelöst
(9) v = vmax [S] / kM + [S]
Diese Formulierung ist als Michaelis-Menten-Gleichung bekannt. Sie beschreibt die Beziehung zwischen enzymatischer Reaktionsrate und der Substratkonzentration, wenn vmax und kM bekannt sind; kM kann man errechnen, wenn man vmax und [S] kennt.
Betrachtet sei hier ein Spezialfall:
v = 1 / 2 vmax
dann wäre
(10) vmax / 2 = vmax [S] / kM + [S]
dividiert durch vmax ergibt
(11) 1 / 2 = [S] / kM + [S]
oder umgeformt
(12) kM + [S] = 2 [S]
kM = [S]
Daraus wiederum ersehen wir, daß die Michaelis-Menten-Konstante kM die Substratkonzentration angibt, bei der die Reaktionsgeschwindigkeit die Hälfte ihres Maximums erreicht hat. Die Dimension von kM ist daher natürlich Mol. Je niedriger der kM-Wert liegt, desto höher ist die Affinität eines Enzyms zu seinem Substrat.
Da der kM-Wert aus einer asymptotisch verlaufenden Kurve nur ungenau ablesbar ist, ist es sinnvoll, die Michaelis-Menten-Gleichung umzuformulieren und in reziproker Schreibweise darzustellen:
(13 ) 1 / v = 1 / vmax [S] / (kM + [S]) = kM + [S] / vmax [S]
Dann ist
(14) 1 / v = kM / vmax [S] = [S] / vmax [S]
oder
(15) 1 / v = (kM / vmax) x 1 / [S]
Diese Darstellung ist als Lineweaver-Burk-Gleichung bekannt. Ihr Vorteil ist die graphisch günstigere Darstellung der Werte. Bei doppelt reziproker Darstellung erhält man eine Gerade mit der Steigung
kM / vmax
1 / kM und 1 / vmax sind die Schnittpunkte der Koordinaten.
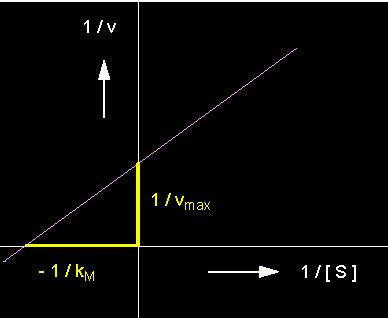
Die Abhängigkeit der Geschwindigkeit einer enzymatisch katalysierten Reaktion von der Substratkonzentration. Doppelt reziproke Darstellung von v und [S] nach Lineweaver und Burk.
Damit wird deutlich, daß ein Enzym zwar die Umsatzgeschwindigkeit einer Reaktion steigert, doch keinen Einfluß auf das Gleichgewicht der Reaktion selbst hat. Diese unterliegt bekanntlich den Konzentrationen, in denen die Reaktionspartner vorliegen (Massenwirkungsgesetz). Damit hat ein Enzym auch keine Wirkung auf das delta G (die freie Energie).
|
|