A variant of the reaction-diffusion model proposed by Gierer
and Meinhardt [Gie1972] (see also
[Mei1982]) was adopted by Meinhardt
[Mei1984] and Meinhardt and
Klinger [Mei1987a, Mei1987b] to capture pigmentation patterns
in seashells.
In this case, the reacting substances (called the activator
and substrate or the activator and inhibitor, depending on the variant of
the model) diffuse in one dimension, along the growing edge of the shell.
One possible set of equations describing this process is shown in
Plate 4.
The observed pattern depicts the evolution of morphogen
concentrations over time, as illustrated in
Plate 5.
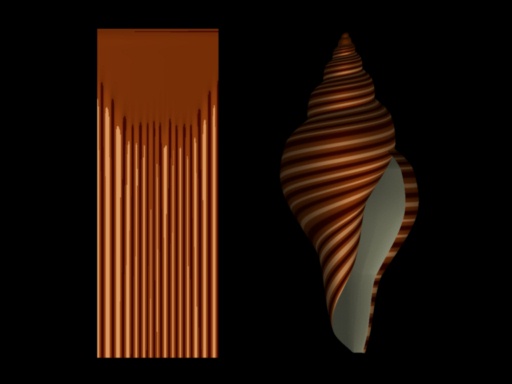 The image on the left shows the distribution of the areas
of low and high concentration of the activator in a plane with time progressing
from the top of the image down. After an initial period, a stable pattern
of areas with low and high concentrations develops, resulting in a series
of parallel lines. In a real shell, the growing edge is curved. A stable
distribution of regions with low and high concentration of the activator
along the edge results in a series of stripes perpendicular to the growing
edge, as shown in the hypothetical shell on the right side of
Plate 5.
Using a different set of parameters, the model can produce
a pattern that is not stable over time, but oscillates. If all points along
the growing edge are in the same state of activation at the same time, the
pattern consists of a sequence of stripes parallel to the growing edge of
the shell, as shown in Plate 6.
Here the shell on the left side of the picture is a digitized
image, and the one on the right is a model. By further modifying the values
of parameters, the model can enter a mode in which some points of the growing
edge are in a stable state of high concentration of the activator, producing
lines perpendicular to the growing edge of the shell, while some other points
oscillate.
 This is illustrated by the model of the Bednall's volute
shell shown in Plate 7.
| 