Historically, the first model of morphogenesis was proposed
by Alan Turing [Tur1952], and is
known as the reaction-diffusion model. The model operates in a plane, as
shown in Plate 1.
Plate 1
: Principle of the reaction-diffusion
model
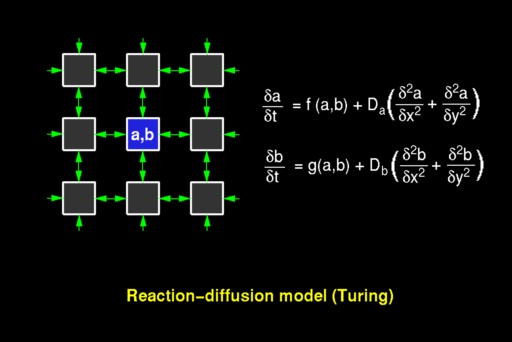 Each point of this plane is characterized by
two numbers, representing concentrations of substances (morphogens) a
and b. A system of coupled partial differential equations describes
changes of these concentrations over time. The substances diffuse and react
with each other.
In the equations, the reaction components are captured
by functions f and g, and the diffusion components
are represented by the remaining terms. The original intent of the reaction-diffusion
model was to explain the ``breakdown of symmetry and homogeneity'' or the
emergence of a pattern in an originally homogenous medium.
An example of this process, using a variant of the reaction-diffusion
model proposed by Young [You1984],
is shown in Plate 2.
Plate 2: Pattern emergence
|
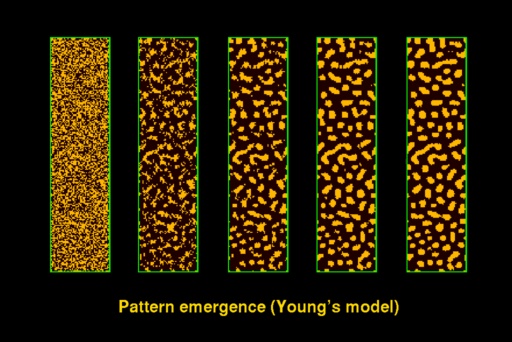
In a sequence of steps, the areas of high concentration (yellow)
become clustered, producing a pattern of light blotches in a dark background. |
| Plate 3
illustrates the effect of varying model parameters on the final pattern.
In nature, the pattern on the right-hand side can be found, for example,
in feathers of some birds, and the middle pattern can be found in the rabbit
fish (as noticed and modeled by Camazine [Cam1993]). |
Plate 3: Activator-inhibitor patterns
 |
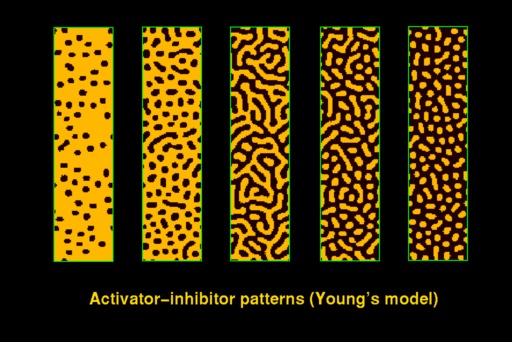The idea of using reaction-diffusion models for image synthesis
purposes was introduced at Siggraph 1991 by Witkin and Kass [Wit1991],
and Turk [Tur1991], who applied it
to generate synthetic animal coat patterns. |
