1. 
2. Help
3. Log In

Musterbildung

Gradienten, Felder und Netze

A. GIERER und H. MEINHARDT (Max-Planck-lnstitut für Virusforschung, Tübingen) haben sich seit Mitte der sechziger Jahre mit biochemischen und mathematischen Grundlagen befaßt, die einer Musterbildung zugrunde liegen. Sie bearbeiteten ursprünglich die Frage nach der Induktion der Kopfbildung beim Süßwasserpolypen (Hydra), denn es war schon lange bekannt, daß Kopfbildung (und Sprossung) nur in einem Mindestabstand von einem bestehenden Kopf erfolgt. Eine solche Beobachtung steht nicht isoliert da. Vielmehr gilt die allgemeine Regel, daß in Nachbarschaft einer Anlage (z.B. eines Organs) keine zweite gleichartige Anlage entstehen kann, da es so etwas wie eine laterale Inhibition gibt, die mathematisch am einfachsten durch das Zusammenwirken eines Aktivators und eines Inhibitors zu erklären ist.

Dabei fällt dem Aktivator eine doppelte Funktion zu: einmal seine eigene Aktivität (oder Synthese) zu steigern (= positive Rückkopplung), zum anderen die Aktivität (oder Synthese) eines Inhibitors zu forcieren. Dem Inhibitor wird nur die Aufgabe zugeschrieben, die Aktivität des Aktivators zu unterdrücken; zudem sollte er sich in einem Gewebe schneller als der Aktivator ausbreiten können. Dafür ist eine höhere Diffusionskonstante erforderlich, und diese wiederum ist mit der Molekülgröße korreliert. Je kleiner nämlich ein Molekül ist, desto beweglicher ist es; in der Regel ist ein kleines Molekül aber weniger spezifisch als ein großes. Das beschriebene Modell repräsentiert einen Regelkreis. Es ist gegenüber einem einfachen Steuerungsprozeß - wie anfangs für die Gradientenbildung beschrieben - durch eine höhere Stabilität (Selbstverstärkereffekt) gekennzeichnet.
Ein Beispiel für Steuerung wäre auch die phototrope Krümmung einer Avena-Koleoptile Bei einseitiger Belichtung der Koleoptilspitze krümmt sich die Koleoptile auf die Lichtquelle zu, weil sich im Gewebe ein Auxingradient ausbildet. Nach Wegfall des Signals bricht er in sich zusammen, das Koleoptilwachstum geht in anderer Richtung weiter.

Eine laterale Inhibition findet man weit verbreitet sowohl im Tier- als auch im Pflanzenreich, sie dient unter Zugrundelegung des obengenannten Modells einer Signalverstärkung (Amplifikation). Zonen hoher Aktivität stehen daher in regelmäßigem Wechsel mit indifferenten Zonen. Das Verhalten der postulierten Größen - Aktivator und Inhibitor - ist durch zwei nichtlineare, partielle Differentialgleichungen beschreibbar:

1. delta a / delta t = rho₀ rho + c rho [a² / h] -my a + D_a [delta² h] / delta x ²

2. delta h / delta t = c rho a² - Dh + D_h [delta²] h / delta x₂

wobei a = Konzentration des Aktivators, h = Konzentration des Inhibitors ist. Beides sind Funktionen der räumlichen (oder zeitlichen) Position. a² steht für die Doppelfunktion des Aktivators, 1/h für die des Inhibitors, und my für Degradationsfaktoren (Rate des enzymatischen Abbaus von Aktivator bzw. Inhibitor).

D_a ist die Diffusionskonstante des Aktivators, D_h die Diffusionskonstante des Inhibitors, rho die Häufigkeit der Zellen, in denen Aktivator bzw. Inhibitor produziert wird und rho₀ entspricht der Background-Aktivator-Produktion

Die aufgestellten Differentialgleichungen sind lösbar. Bei Einsatz "angemessener" Werte erhält man, je nach Wahl der Parameter und der Ausgangssituation, unterschiedliche Lösungen. Veränderungen als Funktion der Zeit lassen sich mit Computerhilfe durch Iterationen simulieren und die Lösungen der Gleichungen repräsentieren Strukturmodelle, die die Entwicklung von Mustern in Raum und Zeit widerspiegeln.

Oszillierende Verteilung von Aktivator (rot) und Inhibitor (blau). In jeder Periode erhält man auf kurze Abstände eine Aktivierung, auf lange (bis zum Beginn der neuen Periode) eine Hemmung, (H. MEINHARDT und A. GIERER, 1974).

Es können Kriterien angegeben werden, die für die Ausbildung stabiler Muster erforderlich sind, außerdem solche, die instabile (statistische) Verteilungen hervorrufen (H. MEINHARDT und A. GIERER, 1974). So läßt sich u.a. die Bildung von Blattanlagen während des Sproßwachstums der Pflanze simulieren oder die Verteilung in einem zweidimensionalen Feld, wie wir sie bei Pflanzen u.a. bei der Verteilung von Schließzellen oder Haaren auf Blattoberflächen finden. Die statistische (stochastische) Verteilung beruht dabei immer auf einer lokalen Instabilität des Aktivator-/Inhibitor-Gleichgewichtszustands.

Anlage von Aktivatormaxima (hier: Blattanlagen) in einem wachsenden Pflanzensproß. Wachstum wird durch Verdopplung der Zellen am oberen Ende des Zylinders simuliert. Die Lage des ersten Maximums ist zufällig. Sie bestimmt jedoch die Lage der nachfolgenden Maxima. Diese können in bestimmten Winkeln (60°, 90°, 120° usw.) und Abständen (wechselständige Blätter) oder im Winkel von 180° (gegenständig) angelegt sein (H. MEINHARDT, 1974).

Wozu das Ganze? Solche Modelle geben wertvolle Hinweise bei der Suche nach morphogenen (gestaltbildenden) Induktoren. Mit Computermodellen kann man so lange rechnen, bis das gewünschte Ziel erreicht ist und das Modell die in der Natur auftretenden Strukturen bestmöglich widerspiegelt. Die Berechnungen müssen von der Größe der Organanlage, der Zahl und Größe der Zellen u.a. ausgehen. Wenn diese Werte zur Verfügung stehen, können die Diffusionskonstanten von Aktivator und Inhibitor ermittelt werden und wenn man diese kennt, hat man bereits einen Anhaltspunkt über ihre Molekulargewichte und kann sie dann bei der biochemischen Suche nach den Substanzen berücksichtigen.

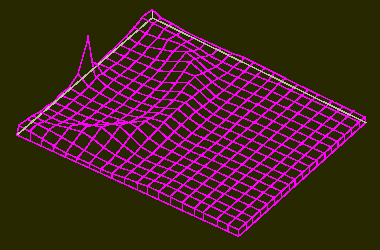
Aktivatormaxima in einem zweidimensionalen Feld (z. B. Blattoberfläche).

a. das System wird durch einen Überschuß an Aktivator an einer Stelle des Feldes in Gang gesetzt. In einer Entfernung, die größer als die Reichweite des Inhibitors ist, erscheint eine ringförmige Zone mit hoher Aktivatorkonzentration.

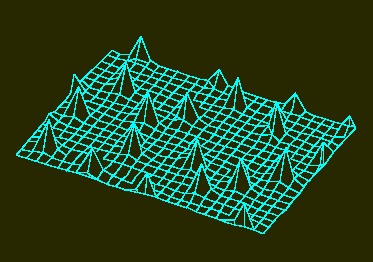
b. Die Struktur ist jedoch instabil und zerfällt anschließend in eine Reihe von einzelnen Aktivatormaxima. Die Aktivatormaxima entwickeln sich in bestimmten Abständen voneinander. Die Verteilung ist zufällig. Man erhält sie in einem nichtwachsenden Feld mit geringen statistischen Fluktuationen der Aktivatorkonzentration in der Anfangsphase (H. MEINHARDT, 1974).

Eine weitere Extrapolation: Blätter sind von einem Blattadernetz durchzogen. Im nebenstehenden Bild ist die Blattnervatur eines tropischen Farns (cf. Asplenium) zu erkennen. Es handelt sich dabei um ein Präparat, das unter natürlichen Bedingungen mazerierte, Parenchym- und Epidermiszellen sind zerfallen, die xylemhaltigen Elemente blieben erhalten.

In der Regel zweigen von einer Hauptader in bestimmten Winkeln Nebenadern ab, die wiederum Ausgangspunkte weiterer Verzweigungen sind. Wie entstehen nun aber solche Netzwerke, und wie kommt es, daß trotz deutlich erkennbarer artspezifischer Unterschiede bestimmte Grundmuster eingehalten werden?

H. MEINHARDT (1976) schlug als Erklärung einen relativ einfachen Mechanismus vor , der auf einer Weiterführung der gerade besprochenen Theorie der Musterbildung beruht. Benötigt wird dazu zunächst einmal eine lokal hohe Konzentration an Aktivator (A); dazu ein Inhibitor (I), von dem angenommen wird, daß er sich an den Rändern wachsender Gewebe (im Meristem) konzentriert und damit einen Auflaufeffekt hervorruft. Der Aktivator dient als Signal für eine Zelldifferenzierung. Die differenzierte Zelle nimmt folglich neue Eigenschaften an, u.a. wird ihr zugeschrieben, die Produktion des Aktivators zu unterdrücken und das Signal, das zu seiner Bildung benötigt wurde, abzustoßen. Die Aktivatorbildung erfolgt darauf in der Nachbarzelle, welche sich dadurch ebenfalls differenziert. Die beiden Zellen nehmen anschließend Kontakt untereinander auf und initiieren damit die Bildung einer Linie. Durch die abstoßende Wirkung auf die Aktivatorproduktion wird sein Bildungszentrum somit vor einer sich kontinuierlich verlängernden Linie vorweggeschoben.

Um nun auch noch zu einem Netz zu gelangen, sind neben Verzweigungen auch noch Rückverknüpfungen erforderlich. Dazu wird eine dritte Komponente - S - mit einer Kontrollfunktion benötigt, von der man annimmt, daß sie sich überall im Gewebe befindet, durch eine sich bildende Linie aber zerstört wird, so daß um jede differenzierte Zelle ein Konzentrationsabfall von S eintritt. Unter der weiteren Annahme, daß die Aktivatorproduktion durch S stimuliert wird, wandert das Aktivitätsmaximum in Zonen mit hoher S-Konzentration. Linien bilden sich deshalb vornehmlich in der Mitte eines Gewebes, wohingegen Randbereiche gemieden werden. Nachdem sich eine Linie um einen bestimmten Betrag verlängert hat, reicht die von der Spitze ausgehende Hemmwirkung (S-Zerstörung) nicht mehr aus, um schwache, entlang der fertiggestellten Linie entstehende Aktivitätsminima zu unterdrücken. Sie treten daher vornehmlich in Bereichen hoher lokaler S-Konzentrationen auf und induzieren damit eine Abzweigung. Bei einer genügend großen Distanz kann eine zweite Abzweigung begonnen werden usw. Die Ausbildung von Linien ist durch das Bestreben, Abstand vom Rand zu halten, gekennzeichnet. Das sich bildende Netz zeichnet sich durch eine hohe Stabilität aus. Entfernt man z.B. alle differenzierten Zellen einer Hälfte, so regeneriert es sich. Das Regenerat ähnelt dem ursprünglichen Muster, ohne ihm direrekt zu gleichen. Die meisten der Verzweigungen enden blind, Rückverknüpfungen sind in der Natur und im Modell selten. Sie kommen gelegentlich aber doch vor und lassen sich durch ein Zusammenspiel der beiden Hemmfaktoren (S-Verarmung, I-Anreicherung) erklären. S-Verarmung an einer existierenden Linie ist der schwächere Faktor, eine wachsende und eine existierende Linie stoßen sich daher weit weniger ab als zwei aufeinander zu wachsende Linien.

Was geschieht, wenn man bei der Modellbildung auf den Faktor S verzichtet? Ein solches Modell würde gabelförmige (dichotome) Verzweigungen hervorbringen, Rückverknüpfungen könnten nicht entstehen. Die Folge davon sind mechanisch instabile Strukturen. Dichotome Blattaderverzweigungen sind evolutionär älter als komplexe Netzwerke. Man findet sie u.a. bei den Pteridophyten und Gymnospermen, während komplexe Netzwerke für Angiospermen typisch sind.

Module und Schalter

Die soeben besprochene Musterbildungstheorie nach GIERER und MEINHARDT demonstriert, wie durch die Ausbildung stabilisierter Gradienten unterschiedliche Aktivitätszonen in zunächst einheitlich gestalteten Feldern entstehen. Sie besagt aber nicht, in welcher Weise sich Zonen in Aktivitätsmaxima oder -minima weiter entwickeln. Die in der obigen Abbildung gezeigte Verteilung von Aktivitätsmaxima kann sowohl zur Ausbildung eines Haarmusters auf einer Insektenoberfläche führen, sie kann aber auch das Verteilungsmuster von Spaltöffnungen auf einer Blattunterseite beschreiben. Das in der obigen Abbildung skizzierte Netz gilt gleichermaßen für Blattaderung wie für den Verzweigungstyp von Blutkapillaren in einem Vertebraten.

Die regelmäßigen Muster, die einer pflanzlichen Entwicklung und den pflanzlichen Phänotyp zugrunde liegen, lassen sich durch die Annahme deuten, daß die geringstmögliche Anzahl an Entscheidungen zu ihrer Bildung zu treffen waren. Hierzu wurden in den letzten Jahren eine Anzahl an Modellvorstellungen entwickelt (u. a. LINDENMEYER, 1971, 1975, 1984, FRIJTERS, 1978). Alle Modelle arbeiten mit einer geringen Zahl an Modulen (sich wiederholenden Einheiten), Kombinationen von Modulen, Iterationen von Modulen und Iterationen von Modulsätzen.

Aufbau eines Pflanzensprosses aus Modulen. Ein Signal (blau) breitet sich von der Basis zur Spitze aus (akripetal)

LINDENMEYER (1971, 1975) definiert die Morphogenese auf molekularer Ebene im Sinne einer Aggregation von Makromolekülen zu größeren Strukturen, wie Membranen, Mikrotubuli oder Geißeln. Die aggregierten Strukturen dienen ihrerseits der Determination der Form von Zellen und Zellorganellen, sie beeinflussen darüberhinaus die Richtung der Zellteilungen, die Zellvergrößerung und zelluläre Transportvorgänge. Zellgruppen agieren wie eine Einheit, sie bilden Gewebe und Organe. Auf diese Weise kommt man schließlich zur Beschreibung von Wachstumsvorgängen des Gesamtorganismus auf morphologischer Ebene. Eine komplette Beschreibung eines sich entwickelnden Organismus müßte die essentiellen Prozesse und Strukturen in der richtigen Zeitsequenz auf allen Ebenen der Organisation enthalten. Da die Zellen bei allen höheren Organismen die einzigen autonomen Einheiten mit genetischer Kontinuität sind, muß man sie auch als die elementaren Einheiten aller Entwicklungsprozesse betrachten. Das Hauptproblem dabei ist, herauszufinden, welche Art einer Instruktion nötig ist, um sie in einer zeit- und raumabhängigen Konstellation zu verändern, sie also zur Teilung anzuregen, zur Größenzunahme, zum Absterben oder zu einer Differenzierung. Es gibt darauf keine eindeutige Antwort, denn die erforderlichen Algorithmen können sich auf verschiedene Weise manifestieren. Unterschiedliche Algorithmen können zudem zum gleichen Ergebnis führen. Die Aufklärung eines Satzes an Instruktionen ist daher keine ausschließlich geltende Erklärung eines Entwicklungsprozesses.

LINDENMEYERs Modell eines vielzelligen Organismus besteht aus einer Abfolge von Symbolen, wobei jedes Symbol eine Zelle repräsentiert, deren Entwicklung algorithmischen Regeln folgt, die eine Substitution von Symbolen zulassen; jedes Symbol folgt eigenen Regeln. Die Substitutionen drücken Vorgänge wie Zellteilungen, Zelltod oder Wechsel des Differenzierungsstatus aus. Sie können durch das Verhalten benachbarter Zellen beeinflußt sein (Abhängigkeit von Zell-Zell-Interaktionen), oder nur vom Status der Zelle selbst abhängen (Entwicklung ohne Zell-Zell-Interaktionen). Durch wiederholten Einsatz eines Algorithmensatzes kann somit eine Sequenz von Entwicklungen simuliert werden. Zusätzliche Kontrollmechanismen dienen der Modulation der aufgezeigten Vorgänge, so daß eine Hierarchie von Abläufen zustandekommt. Das Modell dient vor allen dazu, das Verhalten von Zellnachkommenschaften (cell linages) zu deuten, und ihren Stellenwert im Gesamtsysten zu beschreiben. Jede Zelle kann ihren Status - zumindest prinzipiell - wiederholte Male ändern, sie kann sich z.B. äqual oder inäqual teilen. Hierdurch lassen sich Modelle kreieren, die etwa einem ganzandigen oder einem unterteilten Blatt ähneln. In diesem Fall beruht das Modell auf der Annahme, daß alle Zellen eines Blattes aus einer Zellreihe im Blattprimordium entstehen. Um die Blattform entstehen zu lassen, müssen nur die Zustände der Zellen am sich bildenden Blattrand betrachtet werden. Es bedarf hierzu nur fünf zellulärer Zustände (Wiederholungseinheiten), um die Form eines zusammengesetzten Blattes zu erklären.

Ein Modell, das zusätzlich Zell-Zell-Interaktionen (Transport von Molekülen, Diffusion aktivierender Substanzen) berücksichtigt, ist wesentlich flexibler und kann daher zur Deutung der Bildung komplexerer Formen herangezogen werden, Fluktuatioinen können besser ausgeglichen werden (s. a. Netzbildung nach GIERER und MEINHARDT), die entstehenden Formen sind einander zwar ähnlich, sie gleichen einander jedoch nicht. Externe Faktoren wie Licht, Feuchtigkeit, Temperatur, periodische Größen (Tageslänge) u.a. lassen sich mit integrieren.

FRIJTERS präsentierte 1978, auf diesen Überlegungen aufbauend , ein Modell zur Deutung des Verzweigungsmusters von Infloreszenzen. Infloreszenzen bestehen aus einem Satz an Modulen (Internodien, Nodien, Brakteen, vegetativem Apikalmeristem und Blüten) und Schaltern, wie z.B. den Übergang von Apikalmeristem in ein Internodium, Nodium, Blätter, Zweige oder in eine Blüte. Zur Veranschauung sei hier ein elementares Beispiel vorgestellt. Das Apikalmeristem wird durch A symbolisiert. Die Bildung eines Internodiums und einer Blüte sei wie folgt definiert:

A > I (F) A

d.h. es entsteht ein Internodium, eine Blüte (die sich nicht weiter differenziert) und ein neues Apikalmeristem. Diese Instruktion kann wie im nachfolgend gezeigten Modell wiedergegeben, nach sieben aufeinannderfolgenden Schritten zu einer einfachen siebenästigen Infloreszenz führen.

0. A

1. I (F) A

2. I (F) I (F) A

3. I (F) I (F) I (F) A

4. I (F) I (F) I (F) I (F) A

5. I (F) I (F) I (F) I (F) I (F) A

6. I (F) I (F) I (F) I (F) I (F) I (F) A

7. I (F) I (F) I (F) I (F) I (F) I (F) I (F) A

Wird während der Entwicklung nach einem der Schritte ein weiterer Stimulus (ein zusätzlicher Schalter) in das Modell eingeführt, der die Umwandlung von A > F induziert. entsteht eine Infloreszenz mit terminaler Blüte:

0. A

1. I (F) A

2. I (F) I (F) A

3. I (F) I (F) I (F) A

4. I (F) I (F) I (F) I (F) A

- Schalter -

5. I (F) I (F) I (F) I (F) I (F) (F)

Die Größe der Blüten, die Länge der Internodien etc. kann durch einen oder mehrere weitere Faktoren moduliert werden, so daß die Größe der Einheiten entweder nach jedem Schritt abnimmt, oder so, daß die untersten und obersten Einheiten klein, die mittleren groß werden.

Solche modulierenden Faktoren können Hormone sein, deren Ausbreitung im Gewebe durch Gradienten beschreibbar sind. Schalter wiederum repräsentieren ein- oder ausgeschaltete Gene, deren Aktivitäten für die für die Ausbildung der betreffenden Struktur benötigt werden. Man kennt eine Gruppe von Genen mit regulierender Wirkung, es sind die sog. homöotischen Gene , deren Aktivität die anderer Gene beeinflußt. Sie können also durch ihre Aktivität zahlreiche andere Gene (Gene auf einer niedrigeren Hierarchiestufe) aktivieren, so z.B. den Satz an Genen, der zur Ausbildung eines Blütenkreises oder der zur Bildung eines Blattes benötigt wird. Homötische Gene stehen damit auf einer hohen Hierarchiestufe, ihre Wirkung als Schalter determiniert die Ausbildung ganz bestimmter morphologischer Strukturen.

Akripetale und basipetale Ausbreitung eines Signals. Im ersten Fall bilden sich Blüten und Früchte von der Basis einer Inloreszenz zur Spitze hin, im zweiten Fall erfolgt die Differenzierung von der Spitze zur Basis.