1. 
2. Help
3. Log In

Wachstum, Reproduktionsrate

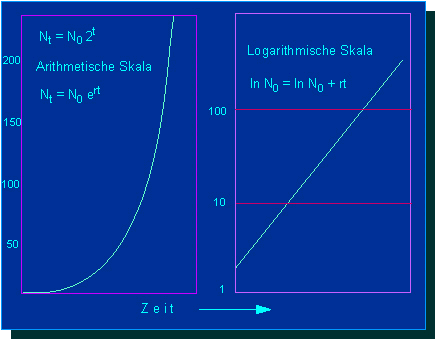
Wachstumskinetik in arithmetischer und logarithmischer Darstellung.

Beginnen wir mit einer Population von N_t Individuen, die zum Zeitpunkt t sehr individuenreich ist. Während eines endlichen Zeitabschnitts (t) ändert sich die Individuenzahl durch Neuzugänge (b) und Abgänge (d) (= Geburten- und Sterblichkeitsrate). Dann ist

delta N_t = (b - d) N_t t ,

wobei die Differenz zwischen b und d als Zuwachsrate definiert ist, die wiederum von der

Zahl der Nachkommen / Generation,

der Anzahl der Generationen / Zeiteinheit

und der Überlebenschance unter gegebenen Umweltbedingungen abhängt.

Vereinfacht lautet die obige Gleichung dann

delta N_t = rN_t t ,

wenn delta t > 0 geht, gilt

delta N_t / dt = rN_t

In integrierter Form geschrieben kommt man zu

rt = ln N_t - ln N₀ ,

wobei N₀ die Individuenausgangszahl und N_t die Anzahl am Ende des Zeitabschnitts dt ist.

Umgeformt lautet diese Gleichung dann

n_t= N₀ e ^rt oder

ln N_t = ln N₀ + rt,

und damit wären wir bei der allgemeinen Wachstumsfunktion, die in ihrer unmodifizierten Form allerdings nur unter idealisierten Bedingungen gilt, z.B. während der logarithmischen Wachstumsphase einer Bakterienkultur oder einer Kultur einzelliger Algen.

Der Teilausdruck er kann mit w gleichgesetzt werden, wobei w die Fitneß (Wrightsche Fitneß) der Individuen symbolisiert. Wird z.B. der Fitneßwert eines Individuums mit 1, der eines anderen mit 2 angegeben, heißt das, daß das zweite doppelt so viele Nachkommen wie das erste erzeugt. Nach r aufgelöst, lautet die obige Beziehung

r = ln w

Die Wachstumsrate ist also gleich dem log naturalis des Fitneßwerts, und der wiederum ist vom Selektionskoeffizienten (s) abhängig

w = 1 - s